8. A CFD elemzés minőségéről és megbízhatóságáról
Ellenőrzés, kalibrálás, validálás
· Ellenőrzés: Jól oldjuk-e meg a leíró egyenleteket? Teljesülnek-e az elvárt konvergencia jellemzők? Eredmények összehasonlítása analitikus megoldással, vagy pontosabb numerikus megoldással.
· Kalibrálás (paraméterezés): Modell fontos paramétereinek behangolása mérési adatok alapján. Illesztés után a modell feltehetően helyesen jelzi előre a módosítások hatását.
· Validálás: Jók-e a leíró egyenletek? Helyesek-e a peremfeltételek? Milyen pontosságot várhatunk a modellünktől? Mérésekhez viszonyítunk.
A legtöbb kereskedelmi forgalomban kapható szimulációs rendszerről feltételezhető, hogy a fejlesztő a kód ellenőrzését már kielégítő mélységben elvégezte.
Összetettebb fizikai modellek tartalmazhatnak olyan paramétereket, (pl. turbulens a Prt Prandtl-szám vagy Sct turbulens Schmidt-szám) amelyekre csak meglehetősen hozzávetőleges szakirodalmi ajánlások állnak rendelkezésre. E paraméterek kalibrálását célszerű a modellezett rendszerre vonatkozó konkrét gyakorlati tapasztalatok (pl. mért teljesítmény adatok) alapján elvégezni. Tartalmazhat a modell további bizonytalan paramétereket is, melyekre szintén visszakövetkeztethetünk a különböző paraméterekkel végzett számítások eredményeinek mérésekkel való összehasonlítása révén. A már kalibrált modelltől elvárható, hogy más fizikai jellemzőkre vonatkozóan is helyes eredményeket adjon, továbbá visszaadja a különféle geometriai és üzemállapotbeli változásoknak megfelelő tendenciákat.
Egy-egy szimulációs módszer vagy megközelítés adott területre való alkalmasságáról mérési eredmények segítségével történő validációval győződhetünk meg. Amennyiben saját mérések elvégzésére nincs lehetőség célszerű hasonló esetekre vonatkozó elemzésék tapasztalatait a szakirodalomban megkeresni. Különféle turbulens áramlási kategóriákra publikus internetes források is találhatók: [ERCOFTAC, 2008]
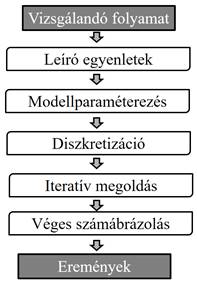
8.1.ábra A CFD elemzésben alkalmazott közelítési lépések
Az áramlások modellezése többlépcsős közelítési folyamat, melynek mindegyik lépe hibák forrása lehet:
· Első lépéseként kiválasztjuk az adott leíró egyenletekkel (transzportegyenletekkel, anyagegyenletekkel, a turbulencia modell kiegészítő összefüggéseivel, reakcióegyenletekkel, stb.) definiált fizikai megközelítést.
· Ezt követően le kell határolnunk a vizsgálati tartományt, definiálnunk kell a szilárd testek alakját és számos más geometriai paramétert. Meg kell választanunk – például mérési vagy tervezési adatok felhasználásával – a vizsgált tér környezetének hatását leíró peremfeltételeket, anyagjellemzőket, esetenként definiálnunk kell szakirodalmi útmutatások alapján további modellparamétereket.
· Következő lépés a diszkretizáció, melynek eredményeként a jelenséget leíró transzportegyenleteket véges számú algebrai egyenlettel helyettesítjük.
· A diszkretizációval nyert algebrai egyenletrendszer közelítő megoldását iterációs módszerrel állítjuk elő, véges számú közelítő lépés alkalmazásával.
· Számításaink pontosságát befolyásolhatja továbbá a valós számok gépi ábrázolásának pontossága is.
Ezeken túlmenően számítanunk kell különféle felhasználói hibákra és programhibákra is.
Különböző alkalmazási területeken eltérőek lehetnek a hibák és bizonytalanságok domináns forrásai. Hiába alkalmazunk például igen sűrű numerikus hálót, ha a peremfeltételek pontatlanságaira, vagy a turbulencia modell alkalmassága befolyásolják jobban a megoldásként keresett fizikai jellemezőket.
A hiba is és bizonytalanság is a modelleredményeknek a pontosnak tekintett értékektől való eltérését fejezi ki.
· Hiba: Az okát ismerjük, szándékos elhanyagolásokból adódik. Az erőforrások növelésével vagy a megoldási módszer fejlesztésével csökkenthető.
· Bizonytalanság: Az ismeretek valamilyen hiányából adódik, ezért nem tudjuk a mértékét becsülni és az erőforrások növelésével csökkenteni.
Bár bizonytalanságok jelenlétében konkrét hibahatár nem adható, a hasonló esetetekre végzett validációs vizsgálatok tapasztalat alapján mégis valószínűsíthető az elérhető pontosság mértéke.
Egyes modellezési feladatok eredménye nem egyetlen konkrét szám (például egy szivattyú szállítómagassága vagy hatásfoka), hanem nagy mennyiségű adat (pl. meteorológiai előrejelzés, vagy a légszennyezők városi terjedése). Ilyen esetekben az is kérdéses, hogy miként számszerűsítsük a modelleredmények és a referencia adatok eltérését. Az eredmények minősítésére alkalmas mérőszámokról részletes áttekintést ad a COST 732 [COST, 2012] projekt keretében készült útmutató.
A CFD legtöbb gyakorlati alkalmazását számos hiba és bizonytalanság terheli, a továbbiakban ezek különféle formáit az alábbiakban röviden tekintjük át. További részletek találhatók a téma szakirodalmában [Slater, 2008].
Modellbizonytalanságnak tekinthetjük a pontos mérésekkel megfigyelhető fizikai jellemzők és a folyamatot leírására alkalmazott alapegyenletek analitikus (pontos) megoldása közötti eltérést.
Oka: Nem jó egyenleteket oldunk meg.
· Turbulencia modellek
· Stacionárius-e az áramlás?
· Ideális gáz, egyéb állapotegyenletek
· Nem newtoni folyadék tulajdonságok
· Reakciómodellek egyszerűsítése
· 2D áramlás
Általános gépészeti alkalmazások esetében a turbulencia modellek bizonytalanságai okozzák a legtöbb fejtörést. Sajnos, az áramkép jó egyezés nem jelenti azt, hogy a turbulens transzport modellje minden egyéb (pl. termikus) vonatkozásban kielégítő lenne.
Jelentős modellbizonytalanságot okozhatnak olyan egyszerűsítő feltevések, mint például ha izotermikus közelítéssel élve figyelmen kívül hagyjuk a hőmérsékletkülönbségek okozta természetes áramlásokat, vagy ha elhanyagoljuk a sugárzásos hőtranszportot. A közelítés okozta pontatlanságokat összetettebb modellek alkalmazásával meg is vizsgálhatjuk, amennyiben az alkalmazott szimulációs rendszer erre módot ad.
A többfázisú és reaktív áramlások szimulációját jelentős modellbizonytalanságok terhelik, meg kell azonban említeni, hogy ezeken a területeken a hagyományos méretezési eljárások is igen pontatlanok, ezért még egy közelítő jellegű szimulációs modell is sokat segíthet a folyamatok megértésében és a technológiai rendszerek tervezésében.
Diszkretizációs hiba alatt az alkalmazott fizikai alapegyenletek analitikus megoldása és a diszkrét modellegyenletek pontos megoldása közötti eltérést értjük.
Oka: Véges sűrűségű háló és véges időbeli felbontás
· Sűrítéssel csökkenthető. A hálókonvergencia rendje a Taylor-sor elhagyott tagjainak nagyságrendjével jellemezhető. Elvileg pl. elsőrendű séma esetében az integrálás hibája a felbontás méretével arányosan csökken, másodrendű séma esetében négyzetével arányosan csökken.
· Időbeli és térbeli diszkretizálásból adódhat.
· Hogy gyakorlatban teljesül-e a konvergencia formális rendje az nem biztos, mert függ a háló minőségétől, upwinding esetében cella Reynolds-számtól, falfüggvény empirikus elemet visz a modellbe stb. A rendet mérni kell.
· Az eredmények hálófüggetlensége szisztematikus sűrítéssel vizsgálható.
A diszkretizációs hiba becslése
Alkalmas módszer lehet például a felbontás kétszeri, lineáris (vonal menti) duplázása. Ennek eredményeként azonban 8-szor, illetve 64-szer több cella keletkezik, tehát a modell memória és számításigénye nagymértékeben megnő. Nem feltétlenül szükséges felezni az intervallumokat, azonban legalább 1.5-szörösére növeljük az intervallumok számát, legalább 3.4-szeresre ezzel a cellaszámot egy-egy sűrítéssel. A különböző felbontású modelleken kapott eredményeinket jelöljük az alábbi módon:
f4h : durva hálós eredmény
f2h : közepes (praktikus) hálóval kapott eredmény
fh : finom hálós eredmény
A sűrítés legyen egyenletes, hasonló háló struktúrát és közel azonos háló minőséget kell biztosítani. Ügyeljünk arra, hogy a falak közelében is azonos arányban kell sűríteni, így azonban kiléphetünk a faltörvények érvényességi tartományából, ami akár egy nagyságrenddel nagyobb hiba forrása is lehet.
A hiba becslésére Richardson-extrapoláció alkalmazható:
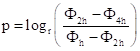 (8.1)
(8.1)
![]() (8.2)
(8.2)
ahol r a sűrítési arány, p a konvergencia mért rendje, f lehet valamely integráljellemző vagy akár mezőváltozó is. Utóbbi esetben a hiba eloszlására is lehet következtetni, így a háló optimalizálható.
Elsőrendű módszer esetében például p=1, egyszeri lineáris duplázás (r=2) esetén a finom hálón kapott megoldás hibája közelítőleg a két hálón kapott megoldás közötti eltéréssel azonos.
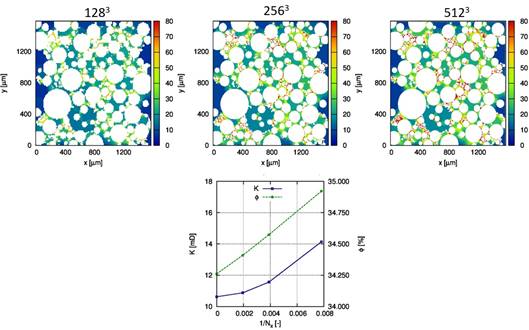
8.2.ábra A Richardson-féle extrapoláció alkalmazása. Fent: áramlási sebesség megoszlása egy véletlen golyóhalmaz szemcséinek környezetében Palabos rács-Boltzmann megoldó segítségével kiszámítva, három eltérő méretű rácson (a csomópontok száma a fejlécben látható). Lent: K áteresztési tényező és f porozitási tényező értékei Richardson-diagrammon ábrázolva. 1/Nx®0 a végtelen sűrű hálóra extrapolált értékeket jelenti.
A numerikus háló kapcsán említett diffúziós hiba például a diszkretizációs hiba egy megjelenési formája.
Általában, adott elemszám esetében is jelentősen csökkenthetjük a diszkretizációs hiba mértékét megfelelő lokális sűrítések és fali háló alkalmazásával, a hálóminőségi paraméterek javításával, továbbá a háló áramvonalasításával. A háló ilyen értelmű optimálását a hálófüggetlenség vizsgálata előtt kell elvégezni.
Amennyiben valamely mezőváltozó (helytől függő) hibáját kívánjuk meghatározni, p értékét célszerű nem lokálisan (helytől függő módon), hanem valamilyen alkalmasan értelmezett átlagértékként meghatározni a tartományra. Rákai [2013] e problémakört áttekinti és alkalmazást bemutatja városon belüli szélmező és szennyező terjedésvizsgálatokra.
A Richardson-extrapoláció nem csupán hibabecslésre alkalmas, hanem az eredmények pontosítására is. Erre láthatunk példát a 8.2.ábrán. A módszerről további részletek találhatók a véges térfogatok módszerének szakirodalmában [Ferziger, 2002].
Az eredmények hálófüggetlenségét minden konkrét alkalmazásnál legalább egyszer célszerű megvizsgálni. Ha az erőforrások nem teszik lehetővé finomabb háló készítését, akkor próbálkozzunk durvább hálóval: ha a durvább hálón látványosan rossz eredményeket kapunk úgy feltehető, hogy a finom hálón végzett számításunk pontatlan.
Iterációs hiba alatt a bekonvergált megoldás és a véges számú iterációval kapott megoldás közötti eltérést értjük.
· Kérdéses, hogy egyáltalán konvergál-e a numerikus megoldás. Ha nem, az leggyakrabban az alábbi okokra vezethető vissza:
1. Hibás háló;
2. Hibás peremfeltételek;
3. Az alkalmazott turbulencia modellel nem kapható adott esetben stacionárius eredmény. Ebben az esetben időfüggő megoldással érdemes próbálkozni. (URANS, SAS, stb.)
4. Túl nagy értékű forrástagok vagy túlságosan merev peremfeltételi egyenletek.
· Figyeljük a reziduumokat! Az első néhány iterációs lépés kivételével az iterációs hiba közel arányosan változik a reziduumokkal: a kezdeti reziduum értékét 10-3, 10-6-szorosára csökkentjük. Vannak olyan esetek, amikor a reziduumok kezdeti értéke kicsi, például a zérus sebességű kezdeti feltétel pontosan kielégítheti a kontinuitást.
· Ha bekonvergált, érdemes megnövelni az underrelaxation faktorokat és megnézni, hogy tartja-e a megoldást.
· Célszerű megvizsgálni, hogy más kezdőértékről indítva is ugyanoda érkezik-e az iteráció.
· Vannak nehezen konvergáló jellemzők, pl. ellenállás-tényező. A reziduumokon kívül néhány integrál jellemző alakulását is figyelni kell! Mindig érdemes nyomon követni a vizsgálat célja szempontjából legfontosabb jellemzők konvergenciáját.
· Az iterációs hiba nem csökkenhet a kerekítési hiba határa alá, ezért leállíthatjuk az iterációt, ha a reziduumok 8.3.ábrán látható tipikus trendje az x-el jelölt ponthoz érkezik.

8.3.ábra A reziduumok jellemző változása az iteráció folyamán. X: ebben a pontban az egyenletes konvergencia véget ér, a reziduumok nem csökkennek tovább.
Divergens iterációt okozhat a numerikus háló lokális torzultsága, hirtelen méretváltozásai vagy az elemek túl nagy oldalviszonya. Ezek a problémák legtöbbször kisebb térrészekben, pontszerűen jelentkeznek, ezért a háló minőségét célszerű alaposan ellenőrizni.
A peremfeltételek alkalmazási szabályainak betartása mellett sem biztos, hogy konvergens iteráció elérhető. Divergencia kialakulhat például egy túlságosan nagy ellenállású outlet-vent peremfeltétel alkalmazásakor, vagy egy intake-fan peremfeltétellel modellezett szivattyú jelleggörbéjének egyes pontjaiban. Ilyenkor célszerű megpróbálkozni az relaxációs együtthatók (Underrelxation Factors) csökkentésével, esetleg más módszer alkalmazásával a nyomás-sebesség kapcsolat feloldására.
Érdemes kiemelni, hogy a turbulencia modellek által bevezetett többlet viszkozitás nem feltétlenül elegendő az áramkép stabilizálásához, tehát nem biztos, hogy stabil stacionárius megoldás létezik. Numerikus megoldás során ez a probléma általában úgy jelentkezik, hogy a reziduumok viszonylag nagy értékek körül (alacsony frekvenciával) hullámszerűen ingadoznak. Ilyenkor időfüggő szimulációs módban célszerű tovább folytatni a számítást.
Az iterációs hiba kellő mértékű csökkentése a hálófüggetlenség vizsgálat előfeltétele.
Kerekítési hiba alatt a pontos számokkal számított megoldás és a véges számábrázolással kapott megoldás közötti eltérést értjük.
· Alapértelmezett számábrázolás 4 byte-os (7 értékes jegy), azonban FLUENT-ben dupla pontosságú számokkal is dolgozhatunk.
· Néhány áramlás, ami tudottan érzékeny a kerekítési hibákra:
- alacsony Re turbulencia modellek;
- természetes konvekció kis hőfokkülönbséggel;
- sugárzásos hőtranszport
- keverék modellek alacsony koncentrációval
- nagy egyensúlyi (hidrosztatikai) nyomásgradiens
A hidrosztatikai nyomásgradiens értékét minimalizálhatjuk a referencia sűrűség (vagy hőmérséklet) alkalmas megválasztásával, a referencia sűrűségnek megfelelő hidrosztatikai nyomás ugyanis a megoldó levonja a nyomásmezőből [Kristóf, 2010; Rácz, ????].
Alkalmazási bizonytalanságnak az optimálisan paraméterezett modell és a rendelkezésünkre álló paraméterekkel kiértékelt modell eredményei közötti eltérést értjük.
Oka: Bizonytalan alapadatok
Ennek lehetséges forrásait az alábbiak:
· Geometriai bizonytalanság
· Peremfeltételek és forrástagok bizonytalanságai
· Anyagjellemzők bizonytalanásga
Geometriai bizonytalanság:
· Nem a terveknek megfelelően készítik el a berendezést (gyárthatósági szempontok, kísérleti vizsgálat alapján tovább optimalizálták a geometriát);
· Kis geometriai részleteknek is lehet nagy jelentősége:
- résáram ventilátoroknál;
- fali érdesség, hegesztési varratok.
· Erősen tagolt geometria esetében porózus modelleket alkalmazunk. Ilyen esetekben ügyelni kell porúzus zóna vagy réteg helyes paraméterezésére.
· Terhelés alatt (áramlás közben) a geometria jelentősen változat, például sátortető körüli áramlás, repülőgépek szárnya. Ebben az esetben az áramlásmodell és a mechanikai modell kapcsolt megoldása javasolható.
Peremfeltételi bizonytalanságok:
· Legtöbb esetben például ismerjük a belépő térfogatáramot, azonban a sebességprofil nincs megadva. A belépő turbulens jellemzőkre általában semmilyen információ nincs. (e például valójában nem is határozható meg kísérleti úton.)
· A peremfeltételi bizonytalanságok numerikus érzékenységvizsgálatokkal határolhatók be.
· Olyan nagyra célszerű választani a modelltartományt, hogy ne legyen nagy a peremérzékenység: felvízi oldalon nagyobb, alvízi oldalon kisebb lehet.
· Épületmodellek esetében például ne az ajtóban írjuk elő a légnyomást, hanem egészítsük ki a nyílásokat megfelelő méretű, kívül elhelyezett dobozokkal.
· Az atmoszférikus áramlások rendkívül érzékenyek a belépő sebesség és turbulens profilokra: a turbulens profilokat a sebességprofillal „össze kell csiszolni” [Balogh, ????].
· A nagyörvény szimuláció erősen peremérzékeny: időfüggő, realisztikus belépősebességprofilokat kell megadni, ellenkező esetben a nagyobb számításigény ellenére sem javul a szimuláció pontossága.
· Állandósult csőáramlásra jellemző sebesség, k és e profilok egy rövid csőszakasszal periodikus peremfeltételek alkalmazásával előállíthatók, tehát gyorsan kiértékelhető segédmodell eredményeit felhasználhatjuk egy nagyobb modellhez, a realisztikusabb belépő peremfeltételeiként.
· Épületmodellek esetében, ha a nyílászárók keresztmetszetében állandó nyomást írunk elő, azzal a kontrakció hatását csökkentjük (esetenként teljesen kiküszöböljük), ez a probléma a gépészet egyéb területein is fellép, ezért általában nem célszerű a peremfeltételeket a legszűkebb keresztmetszetben megadni.
Anyagjellemzők bizonytalansága:
· Sűrűségmodell megválasztása: számolhatunk-e állandó sűrűséggel?
A tengerszinten eddig tartósan mért nyomás szélső értékei:
p: 877 – 1079 kPa → 20 % eltérés
T: 253 – 313 K → 22 % eltérés
Célszerű az eredményeket megfelelő dimenziótlanítással sűrűségtől független alakra hozni.
· Változhat-e az anyagösszetétel?
· A viszkozitás erősen hőmérséklet függő lehet, FLUENT-ben csak a normál állapoti értékek vannak táblázva, azonban törtvonalas függvény vagy polinom formájában összetettebb függés is előírható.
· Nem-newtoni folyadékok modellezése esetében legtöbbször méréssel kell meghatározni a reológiai paramétereket, ügyelve arra, hogy a paraméterek csak korlátozott deformációsebesség tartományban érvényesek (ennek megfelelő mérésre van szükség).
· Magas hőmérsékletek esetén a termikus jellemzők (például a fajhő) is erősen függhetnek a hőmérséklettől.
Hibák és bizonytalanságok okai
1. Modell bizonytalanságok
2. Diszkretizációs hiba
3. Iterációs hiba
4. Kerekítési hiba
5. Alkalmazási bizonytalanság
6. Felhasználói hibák
7. Program hibák
Az felhasználói hibák elkerülése szempontjából nyilvánvalóan a gyakorlás a legfontosabb, ezen túlmenően célszerű egy-egy problémát több különböző módon megközelíteni, ne sajnáljuk az időt arra, hogy minden lehetséges esetben elemi számításokkal is meggyőződjünk az eredmények nagyságrendjének helyességéről.