Áramlások numerikus modellezése
elektronikus tankönyv
Szerző: dr. Kristóf Gergely, BME Áramlástan Tanszék
Lektorok:
…
Terjesztésére jogosult: …
…
(2018)
Köszönetnyilvánítás
A szerző ezúton köszöni dr. Régert Tamás és dr. Lohász Máté hozzájárulását a tantárgy kialakításában, tovább mindazok hozzájárulását, akik az alkalmazási példaként bemutatott elemzésekben közreműködtek. Köszöni dr. Hős Csaba és dr. Lajos Tamás figyelmes lektori munkáját, melyet baráti szívességként vállaltak el. Nagyon köszönöm Csaba Klajbár és Németh Lőrinc hallgatóknak, hogy véleményükkel segítették az anyag fejlődését.
1.
Bevezetés
Napjainkban a gépészeti gyakorlat számos területén, így járműiparban, energetikában, épületgépészetben, környezettechnikában, vegyiparban és egyéb technológiai folyamatok tervezésében az áramlások numerikus modellezése (Computational Fluid Dynamics - CFD) elfogadott módszernek számít. A módszer lényege, hogy az áramlás állapotát meghatározó mezőváltozók térbeli és időbeli eloszlásait az alapegyenletek numerikus megoldása útján határozzuk meg.
A Numerikus áramlástan alkalmazásai
1. Problémák feltárása tervezéskor
2. Ellenőrzés
3. Optimális méretek meghatározása
4. Tervezést segítő korrelációk
5. Üzemeltetési problémák megoldása
6. Környezeti hatások feltárása
7. Optimális szabályzás
Komplex mérnöki tervezési feladatok esetében mindig felvetődnek olyan kérdés, mint Megtaláltuk a rendszer kritikus pontjait? Le tudjuk fedni az összes előforduló üzemállapotot? A CFD elemzés egyik fontos szerepe, hogy átfogó képet ad a működésről, teljeskörű ellenőrző szerepet tud betölteni. Már egy viszonylag durvább modell alkalmazása is elkerülhetővé teszi az esetleges figyelmetlenségből eredő tervezési hibákat.
Az aerodinamikai szabványokban foglalt egyszerűsített számítási módszerrel végzett tervezés néha jelentős túlméretezéshez vezet, például épületekre ható szélerő esetében. Sok esetben azonban, az egyszerű méretezési módszer alternatívájaként a szabványok elfogadják a laborkísérletet vagy CFD elemzést is. Épületek tűzvédelmi rendszerének ellenőrzésére kötelező CFD elemzést végezni a hazai szabályzat szerint.
A CFD modell módot ad a tervezőnek a legjobb megoldás módszeres megkeresésére. Ez főképpen a geometriai paraméterek esetében jelent kihívást, mivel paraméterváltozások esetén az elemzés teljes folyamatát meg kell ismételni a geometria modell előállításától kezdődően. A CFD elemzés jelentős számításidővel jár egy-egy modellváltozat esetében, ezért az optimalizálást általában a minimális számú vizsgálandó változat kiválasztására irányuló kísérlettervezés előzi meg. Az egyes változatok modelleredményei alapján a célfüggvény kiértékelhető, majd az így kapott pontokra analitikus válaszfelület illeszthető a paraméterek által alkotott térben. Ezt követően az optimális paraméterkombináció már gyorsan megtalálható a válaszfelület szélsőértékhelyeként.
A különféle rendszerelemek hidraulikai jellemzőit, például csőelágazások veszteségtényezőjét, mérési adatokra illesztett korrelációk alapján szokás a hálózatmodellekben figyelembe venni. Ennek hátránya, hogy a mérés alapú korrelációk jellemzően korlátozott paramétertartományban érvényesek, továbbá a különböző tartományokban érvényes korrelációk nem csatlakoznak folytonosan egymáshoz. CFD elemzés lehetővé teszi a paramétertartomány teljes mértékű lefedését és általánosabb érvényű korrelációk illesztését [Tomor, 2016, 2017].
Komplex rendszerekben, főként beüzemeléskor, gyakorta előfordulnak olyan meghibásodások, melyeknek többféle oka is lehet és az eredeti okot az irányítástechnikai rendszerben tárolt mérési adatok alapján nem lehet megállapítani. CFD folyamatmodell segítségével feltárhatjuk az ok-okozati összefüggéseket és megkereshetjük a probléma eredeti okát (Root Cause Analysis).
Terjedési jelenségek – általában szennyezőanyag vagy hő transzport – áll a legtöbb környezeti hatásvizsgálat középpontjában. Ilyen jelenségek CFD alapú elemzésére láthatók példák az 1.1.ábrák alsó sorában.
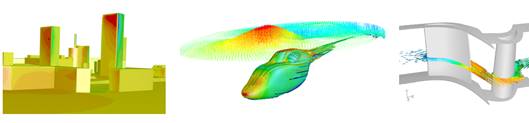
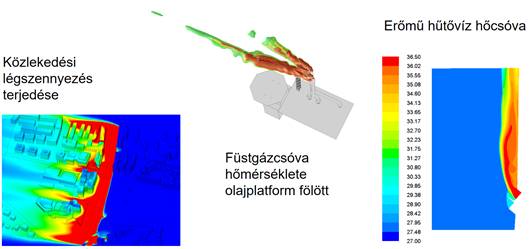
1.1.ábra A CFD néhány gyakorlati alkalmazása
E tananyag a Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Karának BSc képzésében az Áramlástan Tanszék által oktatott numerikus áramlástani témájú, 2 kredites tárgyak tanrendjéhez igazodik. E tankönyv az előadások és laborgyakorlatok anyagát tartalmazza heti 1 + 1 kontakt óra terjedelemben. Elsajátítása a kontaktórákon túlmenően átlagosan heti 1 óra önálló munkát igényel, előtanulmányként Áramlástan [Lajos, 2008] javasolt.
A tantágy oktatási célja az alábbi készségek elsajátítása:
· Szimulációval megoldható műszaki problémák felismerése;
· Alkalmas modellezési megközelítés kiválasztása;
· A szimulációs modell önálló felépítése és kiértékelése ANSYS rendszerben;
· A szimulációs modell megbízhatóságának ellenőrzése.
E tantárgyban a CFD alkalmazói ismereteire helyezzük a fő hangsúlyt. A laborgyakorlatok során ANSYS-FLUENT szimulációs rendszert alkalmazunk, amely kategóriájában élvonalbeli eszköznek számít és a korszerű CFD teljes modellezési eszköztárát magában foglalja. A tananyag az alkalmazott szimulációs rendszerhez nem kapcsolódik szorosan, mivel az ismertetésre kerülő funkciók többsége más szimulációs rendszerekben is hasonló formában található meg. Az elméleti anyagrészben szimulációs platformtól független tárgyalásra törekszünk.
Az ANSYS Fluent-ben fellelhető funkciókat a teljesség igénye nélkül közöljük. Teljeskörű információ az elérhető modellezési lehetőségről a program felhasználói dokumentációjában található. A modellezési funkciók gyakorlati megvalósításának megkönnyítése érdekében a szövegben hivatkozunk a program felhasználói felületének egyes pontjaira, melyek megjelenési formája az újabb programverziók megjelenésével változhat.
Törekedtünk arra, hogy a tankönyv minél pontosabban kövesse az előadást. Az egyes alfejezetek a leglényegesebb tudnivalók összefoglalásával kezdődnek, melyet a szövegben részletesebb magyarázat és alkalmazási példák követ.
Általában előnyös, ha a gyakorlatok az előadásokkal párhuzamosan folynak, ezért a képzés kezdetén még nem áll rendelkezésre a vezetett gyakorlatokban felhasznált funkciók elméleti háttere. Nyilvánvaló, hogy emiatt sok megválaszolatlan kérdés marad az első gyakorlatok elvégzést követően. Fontosnak tartjuk, hogy a gyakorlatok a valóságos műszaki problémák megoldási módszerének megfeleljenek, ezért kérjük szíves türelmét az eleinte ismeretlen funkciók használatakor. Bízva abban, hogy a félév végéig a CFD elemzést érintő minden fontos kérdésére választ talál, sikeres felkészülést kívánok.
Az áramlástani szimuláció módszerei
A három legelterjedtebb módszercsalád:
· Véges differenciák módszere;
· Véges térfogatok módszerek (FVM);
· Végeselem módszer (FEM);
Néhány kevésbé elterjedt módszer:
· Spektrál módszerek;
· Rács nélküli módszerek (SPH);
· Rács-gáz módszerek (LBM).
A véges differenciák módszerének lényege, hogy a folyamatot leíró differenciálegyenletekben szereplő differenciálhányadosokat néhány konkrét pontban felvett függvényértéket felhasználó differencia sémákkal közelíthetjük. E sémákat az alapegyenletbe behelyettesítve algebrai egyenleteket kapunk. A módszer fő korlátja, hogy rendezett térbeli felbontást, struktúrált (rendezett) hálót igényel, így bonyolult geometriai esetekben a numerikus felbontást nem lehet elég rugalmasan illeszteni a megoldás kritikus részeihez, például résekhez, nyírórétegekhez, ahol a megoldást helyileg nagy gradiensek jellemzik.
A végeselem módszer [Páczelt, 2007] szilárd testek mechanikájában egyeduralkodó eljárásnak tekinthető. A módszer erőssége, hogy megfelelő simaságú megoldások esetében igen nagy numerikus pontosság érhető el igen kevés elemmel is. Az áramlástani feladatok sajátossága, hogy modellezés pontossága elsősorban az elemszám növelésével javítható. (Jelenleg például a FLUENT szimulációs rendszer oktatási verziója 500 000 elemre van korlátozva, ami szilárdságtanban meglehetősen nagy elemszámnak számítana, azonban gyakorlati áramlástani probélmák megoldására általában kevés lenne.) A nagyszámú szimulációs elem, sok processzor magon történő parallel feldolgozást igényel. A számítástechnikai fejlődés jelenlegi iránya is inkább a sokmagos processzorok, mint az erősebb processzor magok felé irányul. A végeselem módszerek esetében a parallel számítás napjainkban még - a vezető véges térfogatos szimulációs rendszerekhez képest - igen rossz hatásfokkal működik. Talán ez a legfőbb oka annak, hogy jelenleg áramlástanban a véges térfogatok módszere tekinthető domináns megközelítésnek.
A spektrál módszerek a gyors Fourier-transzformáció alkalmazására épülnek, melynek alkalmazásával a differenciálás és integrálás frekvencia tartományban algebrai műveletekké alakulnak. Különösen előnyösen alkalmazható periodikus tartományban, például a globális meteorológiai modellek esetében. Gépészeti gyakorlatban ritkán alkalmazzák, mert a módszer nem alkalmas struktúrálatlan numerikus hálók kezelésére.
Többfázisú áramlások és keveredési folyamatok modellezésére kiválóan alkalmas rács nélküli módszer a Smmothed-Particle Hydrodynamics (SPH), mely a számítógépes grafikai alkalmazások területéről terjedt át a mérnöki gyakorlatba és napjainkban is dinamikusan fejlődik. A módszer nem igényel numerikus hálót. A folyadékot, mint egymással kölcsönhatásban álló cseppek összességét tekinti. Általános CFD módszerként még nem vehető számításba, mert a numerikus felbontás nem szabályozható megfelelően.
A rács-Boltzmann módszerek a mikroszkópikus részecskeáramokat bontják fel, tehát egy-egy rácspontból minden szomszédos rácspontba terjedhetnek részecskék (irányonként eltérő darabszámban), majd a csomópontokban ütköznek egymással a különböző irányban haladó részecskék. Az áramlási sebesség egy adott pontban a mikroszkópikus részecskeáramok összegzésével áll elő. A módszer rendkívül alkalmas a turbulencia direkt szimulációjára valamint kétfázisú áramlások (pl. víz-vízgőz rendszer) modellezésére, azonban a numerikus háló lokális sűrítése nem megoldott, ezért a mérnöki gyakorlatban kevéssé terjedt el.
A véges térfogat módszer (hasonlóan a végeselem módszerhez) a számítási tartomány kisebb térfogati elemekre bontja, amelyeken belül a keresett áramlástani mezőváltozók egyszerűbb (pl. lineáris) függvényekkel közelíthetők.
A tartomány felbontását hálógenerálásnak, a térfogatelemeket pedig celláknak hívjuk. Mezőváltozóink diszkrét értékeit a cellák középpontjában szeretnénk meghatározni.
Célunk: az áramlást leíró megmaradási egyenletek megoldása közelítő módszerrel.

1.2.ábra V ellenörzőtérfogat és F fluxus a térfogat „A” határfelületén
U: valamilyen megmaradó, azaz zárt rendszerben állandó mennyiség (például tömeg, impulzus vagy energia) térfogati sűrűsége. A folyadék okozta szállítás/terjedés folyamatát az (1.1) általános transzportegyenletben lehet megfogalmazni:
![]() (1.1)
(1.1)
(1.1) összefüggésben V egy tetszőlegesen megválasztott ellenőrzőtérfogatot, A annak kontúrját, t pedig az időt jelöli. F fluxusvektor a megmaradó jellemző az egységnyi felületre (keresztmetszetre) vonatkoztatott áramát jelenti. SV és SA-vektor a térfogati és felületi források, melyek a V térfogaton kívülről származó hatásokat fejezik ki. Az (1.1) transzportegyenlet bal oldalán látható első két tag értelmében: ha egy megmaradó jellemző – az S források következtében – termelődik, akkor két dolog történhet vele: 1) a V térfogatban fölhalmozódik, vagy 2) annak A kontúrján kiáramlik a tartományból.
A transzportegyenletek (1.1) integrál alakját minden szimulációs cellára közelítő integrálokkal alkalmazzuk, így egy-egy cellára vonatkozó algebrai egyenlethez jutunk. Ezt nevezzük térbeli diszkretizálásnak a véges térfogatok módszere esetében.
Térfogati források hiányában egy megmaradó jellemző térbeli megoszlását csak az átrendeződés sebessége, azaz a fluxus-vektor térbeli megoszlása határozza meg. A fluxust két részre bonthatjuk: a folyadéktömeg elmozdulásával összefüggő (tömegáramával arányos) FC konvektív fluxusra, valamint a molekuláris keveredés és az áramlás szimulációs cellaméretnél kisebb struktúráinak okozta keverőhatást kifejező, ezért a megmaradó jellemző f tömegkoncentrációjának gradiensével arányos FD konduktív (diffúzív) fluxusra, tehát
![]() (1.2)
(1.2)
![]()
![]() (1.3)
(1.3)
ahol r a (tömeg)sűrűség, v pedig az áramlási sebesség vektora. (1.3) képleteket (1.1) egyenletbe behelyettesítve az általános transzportegyenlet az alábbi alakra hozható:
![]() (1.4)
(1.4)
A jobb áttekingetőség kedvéért a megmaradási tétel konkrét alkalmazásait differenciál formában mutatjuk be, ezért az általános összefüggést a Gauss–Osztrohradszkij-tétel segítségével az (1.5) differenciál alakra hoztuk.
![]() (1.5)
(1.5)
f mennyiség a különféle megmaradási tételekben az alábbi táblázat szerint értelmezhető:
|
Egyenlet |
f |
|
kontinuitás |
1 |
|
x-impulzus |
u |
|
y-impulzus |
v |
|
z-impulzus |
w |
|
fajlagos energia |
e |
Az egykomponensű folyadék áramlását leíró alapegyenletek – az (1.5) egyenletnek megfelelő, konzervatív (megmaradási) alakban – a következő formát öltik:
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
![]() (1.10)
(1.10)
Felületi erők:![]() (1.11)
(1.11)
Az impulzustétel differenciál alakjában u, v és w az áramlási sebesség x, y és z koordináta irányú komponenseit jelöli, p a nyomás, gx, gy és gz a térerősség vektor egyes komponensei, m pedig a dinamikai viszkozitási tényező (mely SI rendszerben Pa.s mértékegységű). Az energia egyenletben „e” a belső- és mozgási energia összegeként értelmezett, egységnyi tömegre vonatkoztatott torlóenergiát, t a csúsztatófeszültség-tenzort, l a hővezetési tényezőt és T a hőmérsékletet jelöli.
A jobb oldali tagok között felfedezhetjük a forrástagokat és a konduktív fluxus tagokat. A nyomásgradiens például az impulzus felületi forrásának tekinthető. A viszkózus erőket az (1.7-1.9) egyenletekben az impulzus konduktív fluxusaként írtuk fel, ugyanakkor a felületi erők összességét (1.11) képlet alapján összefoglalva a viszkózus erők felületi forrásként is kifejezhetők, mely a t a csúsztatófeszültség-tenzor mozgásállapottól való általánosabb függéseinek figyelemebe vételét is megengedi.
A transzportegyenletek hasonló alakban történő felírása egységes diszkretizációs módszerek alkalmazását teszi lehetővé.
Az (1.6-1.10) transzportegyenletekben különböző indexekkel megtalálható S tagok a megmaradó jellemzők térfogati forrásai (egységnyi térfogatban, egységnyi idő alatt keletkező megmaradó jellemzők), melyek az ANSYS-FLUENT rendszerben a felhasználó szabadon programozhat, így tömeget, erőt, vagy hőt vihet be egy adott térrészbe. S térfogati forrásokat függővé tehetjük időtől, helytől, vagy akár a számított mezőváltozók (például az áramlási sebesség vagy a hőmérséklet) pontbeli értékétől. Az S forrástagokat felhasználhatjuk olyan hatások figyelembevételére, melyeket a numerikus felbontás nem tenne lehetővé, például a porózus anyagok hidraulikai ellenállásának számítására, vagy egy finom bordázatú hőcserélő által bevitt hő figyelembevételére.
Összetettebb fizikai problémákat is megoldhatunk hasonló alakú további transzportegyenletek beiktatásával. A folyadékkomponensek koncentrációjára felírt transzportegyenletekkel például reaktív áramlások modellezhetők, ha adottak az egyes komponensek képződési rátáit (tömegforrásait) leíró összefüggések. Később látni fogjuk, hogy az egyes folyadékrészek turbulencia jellemzői is meghatározhatók hasonló transzportegyenletek segítségével, ezért a legtöbb turbulencia modell 1-7 db. további transzportegyenlettel egészíti ki a fenti rendszert. ANSYS-FLUENT rendszerben a felhasználónak lehetősége van tetszőleges számú további transzportegyenlet megoldására is, melyeket G transzport-tényezők, forrástagok és peremfeltételek számítási módjának megadása révén egyedi fizikai tartalommal tölthet fel (lásd: User Defined Scalar – UDS transzport).
Az alábbiakban összefoglaljuk a véges térfogatok módszerének néhány lényeges sajátosságát:
· A legtöbb véges térfogatos megoldási módszer cellánként csak egyetlen mezőváltozó értéket tárol, melyet a cella középpontjához (cell centroid) rendelünk.
· Az (1.6-1.10) alapegyenletek diszkretizálását az (1.4) egyenletnek megfelelő integrál alakban végezzük el, ezért csak térfogati és felületi integrálokat szükséges közelítő módszerrel kiszámítani. A térfogati integrálokat a középpontban tárolt jellemzők alapján, cellatérfogattal való szorzással kellő pontossággal meghatározhatjuk. A felületi integrálok szomszédos cellák közötti határfelületre képzett elemei kifejezhetők az adott felületben határos két cella középpontjában tárolt jellemzők alapján.
· Minden transzportegyenlet, minden cellára egy-egy algebrai egyenletet eredményez, ezt nevezzük a leíró egyenletek diszkrét közelítésének. A cella határfelületeken a megmaradó mennyiségek áramai csak a helyi és a szomszédos cellában tárolt mezőváltozótól függ, ezért a numerikus „stencil” csak az adott cella első szomszédjaira terjed ki, így a véges térfogatok módszere viszonylag egyszerű algebrai egyenleteket eredményez.
· A diszkretizálás eredményeként nagyszámú algebrai egyenletből álló rendszer áll elő. Tipikus példaként: 5 transzportegyenlet és 1 000 000 cella esetén 5 000 000 db. algebrai egyenletből álló egyenletrendszert kapunk.
· A számítási tartomány határára eső cella-részfelületekre vonatkozó integrálok számításához az elhagyott térrész hatását leíró újabb összefüggések: peremfeltételek megadása szükséges.
· A sok ismeretlen és az egyenletek nemlinearitása miatt az algebrai egyenletrendszer pontos megoldása nem lehetséges, iteratív közelítő eljárásokat alkalmazunk. Azt szeretnénk, hogy a megoldás valamilyen iniciális (kezdeti) állapotból indulva lépésenként konvergáljon a diszkrét egyenletrendszer pontos megoldásához. (Legtöbbször így is történik.)
· Ha a diszkrét egyenletrendszer elemeit a teljes számítási tartományra összegezzük, a belső felületekre képzett felületi integrálok kiesnek, így a megmaradási tételek a teljes tartományra pontosan kielégülnek. A numerikus sémák hibái, tehát nem működhetnek a megmaradó jellemzők forrásaiként: a numerikus módszer konzervatív. Ez a gyakorlati alkalmazás szempontjából igen fontos, ugyanis durva hálón sem kapunk fizikai szempontból teljesen értelmetlen eredményt. A véges térfogatos diszkretizálás természetéből adódóan konzervatív. (Más diszkretizációs eljárások esetében nem mindig érhető el.)
A véges térfogat módszer részletes ismertetése meghaladja e tárgy kereteit. Átfogó jellegű szakkönyvként javasolható: [Ferziger, 2002].

1.3.ábra A CFD munkafolyamat megjelenése ANSYS Workbench-ben
1. Geometriai modell előállítása
2. Hálógenerálás
3. Peremfeltételi zónák kijelölése
4. Fizikai modell kiválasztása, anyagjellemzők megadása
5. Peremfeltételek számértékei
6. Numerikus paraméterek
7. Megoldás inicializálása
8. Iteráció
9. Eredmények értékelése
A geometriai modell előállítása lényegében bármely CAD rendszerben történhet. A gyakorlati példák megoldása során a DesignModeller nevű programot használjuk, mely az ANSYS rendszer által kínált paraméteres CAD rendszer. Az ANSYS rendszerben ugyancsak hozzáférhető a SpaceClaim nevű direkt modellező program, mely a geometriai objektumokat nem az előállítás módszerével, hanem a végső állapotával írja le. Legtöbb gyakorlati esetben a geometriai modellt az áramlástani elemzés előtt egyszerűsíteni kell, a hálózást megkönnyítő darabolást kell elvégezni, melyet a SpaceClaim nagyon megkönnyít. További előny, hogy minden elterjedt CAD rendszerből képes importálni, ezzel szemben hátránya, hogy a SpaceClaim-ben átalakított geometriai modell a paraméteres CAD rendszerekben „elvesznek”. SpaceClaim-ben végzett műveletek makrók segítségével is elvégezhető, így a kiinduló modell frissítése automatizálható.
Hálógeneráláskor beállítjuk a numerikus felbontás finomságát a számítási tartomány egyes részein figyelembe véve a megoldás gradienseinek várható irányát is, például fali határrétegekben a megoldás falra merőleges irányban változik gyorsan, ezért ebben az irányban erőteljesebben kell sűrítenünk a hálót, ami lapos cellák alkalmazását igényli. A sajátos sűrítési követelményeken túlmenően a háló minőségére vonatkozó további követelményeket is figyelembe kell venni. A hálógenerálással kapcsolatos tudnivalókat a 2. fejezetben foglalkozunk.
Hálózáskor jelöljük ki a vizsgált tér és a kontúrfelület azon részeit, amelyeken eltérő peremfeltételeket vagy térfogati forrásokat kívánunk működtetni, vagy akár az eredmények értékelése során kívánunk az adott tartományra jellemző adatokat nyerni (pl. egy felületre ható erő lekérdezésével).
A fizikai modell kiválasztásakor kell meghatároznunk például, hogy az áramlás stacionárius-e, kiválasztjuk a megfelelő anyagmodellt és eldöntjük, hogy megoldjuk-e az energia egyenletet. Legtöbb tapasztalatos az adott vizsgálathoz legmegfelelőbb turbulencia modell kiválasztása és alkalmazása igényli, mellyel a 6. fejezetben foglalkozunk részletesebben.
A peremfeltételek a számítási tartománnyal határos külső tér hatását írják le. Előírhatunk például falat, szimmetriát, periodikus határokat vagy a ki- és beáramlási peremfeltételek különféle változatait. Ezeket a modellezési lehetőségeket a 3. fejezetben részletezzük.
A numerikus paraméterek megadása egyszerű esetekben nem okoz sok fejtörést: az alapértelmezett beállítások túlnyomó többsége elfogadható FLUENT megoldó alkalmazása esetén. Bonyolult fizikai modellekhez nincsen általános érvényű numerikus megoldási stratégia, ezért célszerű a modellt lépésről-lépésre fejleszteni, kezdetben tesztelésre alkalmas, kis elemszámú modelleken tapasztalatot gyűjtve.
Inicializáláskor általában a mezőváltozókat vagy konstans kezdeti értékekkel, vagy potenciálos áramlásnak megfelelő értékekkel töltjük fel.
Az iterációs folyamat során a megoldó lépésenként finomítja a numerikus megoldást. Általában nem látható előre, hogy a kielégítő pontosságú megoldás eléréséhez hány iterációs lépés szükséges. A közelítő megoldás pontosságának tesztelésére az alapegyenletek reziduumai alkalmasak, melyek az aktuális közelítő megoldásnak a diszkrét alapegyenletbe való behelyettesítésével állnak elő. Ilyen módon bármely iterációs lépésben, egy skaláris mezőváltozóra felírt megmaradási tétel, a háló minden cellájában egy-egy reziduum értéket szolgáltat. Az ANSYS Fluent a reziddumok értékét az egész tartományra normálva, továbbá az iteráció kezdetén fölvett értékkel elosztva, logaritmikus skálán jeleníti meg transzportegyenletenként külön-külön (reziduum görbék). A reziduumok csökkenése az iteráció során tehát arra utal, hogy a közelítő megoldás egyre pontosabban kielégíti az alapegyenleteket és azok peremfeltételeit. Az iteráció automatikusan leáll és a megoldó „Solution is converged” üzenetet küld, ha minden megmaradási tétel normált reziduum értéke az adott egyenletre előírt határ (pl. 10-3) alá csökken. ANSYS-FLUENT-ben a szimuláció futása (iteráció) bármikor megállítható. Ekkor módosíthatjuk a numerikus paramétereket, vagy akár a fizikai modell is, majd újrainicializálás nélkül folytathatjuk a szimulációt a korábbi számítás eredményeit kezdeti feltételként felhasználva.
Számos látványos módszerrel értékelhetők a szimulációs eredmények: például testek felületén, vagy metszősíkokban szintvonalas ábrázolást alkalmazhatunk vagy valamilyen skaláris jellemző szerint színezet áramvonalakat jeleníthetünk meg. Egyes felületi integrálok numerikus kiértékelésével megtudhatjuk például adott keresztmetszetben átáramló folyadék térfogatáramát és a testekre ható erőket. A FLUENT saját kiértékelő rendszerrel rendelkezik, emellett az ANSYS rendszerben két tovább kiértékelést segítő program is. A CFD-Post segítségével több számítási eredményt egyszerűen össze is hasonlíthatunk. Az EnSight program segítségével pedig az 1.4.ábrához hasonló igényes, összetett vizualizációk állíthatók elő.

1.4.ábra Áramvonalak egy személyautó nyomában EnsSight segítségével megjelenítve